Eksponentinis augimas

Eksponentinis augimas yra lengvai atpažįstamas iš viršun besiriečiančios kreivės. Štai kaip va šita kreivė, rodanti koronaviruso epidemijos augimą Lietuvoje.

Eksponentinis augimas - tai tokia matematika, kuri pirma beveik neauga, paskui auga labai lėtai, paskui lėtai, paskui vidutiniškai, paskui greitai, paskui labai greitai, paskui labai labai greitai, paskui nenormaliai greitai, o paskui jau pyst ir visai tvoja ir viską užtvoja.

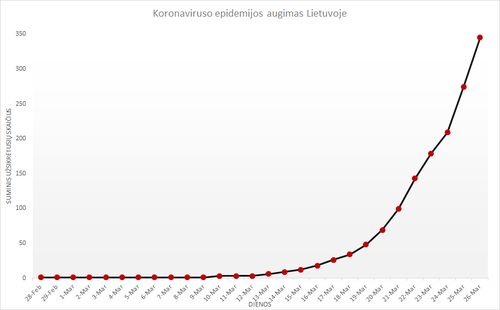
Eksponentinis augimas tapo plačiai nagrinėjama tema, kai visur paplito koronaviruso epidemija. Kadangi šioji plito eksponentiniu būdu, tai daugelis buvo priversti apie tą eksponentinį augimą sužinoti, netgi jei nieko žinoti ir nenorėjo.

Eksponentinio augimo esmė

Eksponentinio augimo esmė - kad jame pagrindą sudaro anksčiau buvusių skaičių dauginimas iš tam tikro prieš tai buvusio skaičiaus. Ryškiausi pavyzdžiai eksponentiniam augimui - tai visokių gyvūnų dauginimasis ir epidemijos. Tiesą sakant, epidemijos irgi yra kokių tai gyvūnų dauginimasis, tiktai dauginasi virusai ar bakterijos. Bet kadangi tai irgi tam tikri gyvi ar pusiau gyvi organizmai, tai jie irgi dauginasi ir efektas gaunasi tas pats.

Bendru atveju eksponentinis augimas yra toksai, kur kiekvienoje iteracijoje prisideda naujas skaičius, gautas iš ankstesnio, jį padauginus iš kažkokio kito. Gaunasi panašiai, kaip kokia geometrinė progresija - kuo toliau, tuo auga greičiau, ir tas augimo greitis didėja tiesiog nevaldomai.

Eksponentinis triušių dauginimasis

Štai eksponentinio augimo pavyzdys su triušiais:

• Turime 2 triušiukus. Bendra triušių suma: 2.
• Ta pora triušių atsiveda 6 triušiukus. Viso šioje iteracijoje atsivesta triušių: 6. Bendra triušių suma: 8.
• Po 6 mėnesių tie 6 triušiukai sudaro 3 poras ir kiekviena iš tų porų atsiveda dar po 6 triušiukus - iš viso jau 18... Senesnė pora irgi atsiveda dar 6 triušiukus. Viso šioje iteracijoje atsivesta triušių: 24. Bendra triušių suma: 32.
• Dar po 6 mėnesių triušiukus atsiveda ir pirma pora, ir kitos 3 poros, ir dar naujos 12 porų, visos po 6 triušiukus. Viso šioje iteracijoje atsivesta triušių: 96. Bendra triušių suma: 128.
• Dar po 6 mėnesių vėl visos tos triušių vados atsiveda triušiukus, kaip ir anksčiau. Viso šioje iteracijoje atsivesta triušių: 384. Bendra triušių suma: 512.
• Dar po 6 mėnesių jau tos visos vados vėl atsiveda triušiukus. Viso šioje iteracijoje atsivesta triušių: 1536. Bendra triušių suma: 2048.
• Dar po 6 mėnesių... Viso šioje iteracijoje atsivesta triušių: 6144. Bendra triušių suma: 8192.
• Ir dar po 6 mėnesių... Viso šioje iteracijoje atsivesta triušių: 24576. Bendra triušių suma: 32768.
• Ir dar po 6 mėnesių... Viso šioje iteracijoje atsivesta triušių: 98304. Bendra triušių suma: 131072.
• O dar po 6 mėnesių... Viso šioje iteracijoje atsivesta triušių: 393216. Bendra triušių suma: 534288.
• O dar po 6 mėnesių... Viso šioje iteracijoje atsivesta triušių: 1572864. Bendra triušių suma: 2107152.
• Galų gale, dar po 6 mėnesių... Viso šioje iteracijoje atsivesta triušių: 6321456. Bendra triušių suma: 8428608.

Kaip matome, per 5 metus iš vienos poros triušių, vos iš 2 padarėlių, prisidaugino daugiau kaip 8 milijonai.

Triušių dauginimasis Australijoje

Triušių pavyzdys pateikiamas būna ne šiaip sau, nes jis yra iš praktinės patirties Australijoje, kuri iki šiol negeba išspręsti triušių problemos.

Viskas prasidėjo 1859 metais, kai kažkoksai Thomas Austin, nutarė, jog nori pamendžioti triušių, nes buvo pripratęs juos medžioti Anglijoje. Taigi, kai persikėlė į Australiją, pasigedo šito užsiėmimo, todėl sumąstė, kad visai neblogai būtų jų užveisti apylinkėse. Sprendimą rado nesunkiai - tiesiog užsisakė iš Anglijos būrelį triušių. Gavęs 24 triušius, juos paleido į laisvę savo ūkyje Barwon Park, kažkur Viktorijos valstijoje.

Negana to, kad tasai Thomas Austin paleido triušius į laisvę, tai dar ir pareiškė, kad "kelių triušiukų įvedimas vargiai padarys kam nors žalos, bet duos prisiminimą apie gimtuosius namus, o tuo pačiu ir malonumą medžioti".

Greitai paaiškėjo, kad triušiai dauginasi neįtikėtinais tempais ir plinta visur, kur tik gali. Australijos sąlygos buvo tiesiog idealios triušių plitimui - jokių plėšrūnų, kraštutinai švelnios žiemos, primenančios ne tiek žiemą, kiek šiltą rudenį, kažkokią bobų vasarą tiesiog. Ir negana to - visur laukai, pilni triušiams tinkamos žolės, visokių daržovių, grūdų ir panašiai, taigi - maisto kiekis tiesiog neribotas. Žodžiu, triušiai galėjo daugintis taip greitai, kaip tik įmanoma.

Praėjus nepilniems 10 metų nuo jų paleidimo 1859, australai tose vietovėse jau sumedžiodavo apie 2 milijonus triušių per metus - ne tiek šaudydami, kiek spąstais. Ir ne tiek dėl medžioklės ar maisto, kiek bandydami apsaugoti nuo triušių savo pasėlius. Nepaisant tokio masinio triušių naikinimo, nesimatė, kad jų populiacijai tai darytų kad ir menkiausią įtaką - jų kiekiai jau buvo dešimtis kartų didesni.

Per vėlesnius metus buvo bandoma taikyti visas įmanomas triušių naikinimo priemones. Triušiai buvo nuodijami nuodais, jų lizdai būdavo užariami ir užakėjami. Buvo sukurti netgi specialūs triušių naikinimo mechanizmai, primenantys akėčias ir plūgus, kurie tiesiog pjaudavo žemę, supjaustydami negiliuose urveliuose besislepiančius triušius. Kai kurie ūkininkai bandydavo ir fosforo deginimą, ir netgi laukų sprogdinimus, tačiau tokios priemonės nebūdavo labai efektyvios, o ir kitų bėdų pridarydavo. Taip pat buvo naudojama masinė medžioklė spąstais, sugautus triušius tiesiog paskui sumalant ir perdirbant į lesalą vištoms.

Kuriam laikui triušių populiaciją pavyko sumažinti tik apie 1950, kai buvo užvežta ir tyčia paskleista triušiams mirtina liga - miksomatozė. Vienok nors triušių populiacija keleriems betams sumažėjo dešimtis kartų, po kiek laiko išsivedė atspari triušių veislė ir jų kiekis atsistatė. Panašiai triušių kiekis atsistatydavo ir po vėlesnių kitų ligų užvežimo. Taigi, triušių problema taip ir liko neišspręsta iki šiolei.

Eksponentinio augimo supratimo sąsajos su mąstymo charakteristikomis

Eksponentinis augimas visiškai nesuprantamas dibilams, nes jis yra kintamas ir netiesinis per visus taškus. Kitaip tariant, dibilai negali suprasti, kaip čia gali būti, kad pradžioje niekas nesiskiria, o paskui skiriasi, o paskui labai baisu. Jiems tai per sudėtingai.

Lygiai taip pat eksponentinio augimo nesupranta ir žmonės, kurie turi humanitarinį mąstymą, nes tam mąstymui nėra suvokiama matematika. Jiems lygiai taip pat nesuprantama, kaip čia dabar pradžioje 1+1, o paskui jau belenkiek daug. Humanitarams tai irgi nesuvokiama.

Iš aukščiau esančių įrodytų teoremų rezultato tapatumo galime daryti išvadą, kad silpnapročiai ir humanitarai yra bent dalinai, o gal ir visiškai persiklojančios aibės.